What is EEMS Online?

EEMS Online is a web-based mapping and modeling system developed by the Conservation Biology Institute (CBI). It is designed to allow the user to explore, modify, and run models constructed using the Environmental Evaluation Modeling System (EEMS; Sheehan and Gough, 2016), a fuzzy-logic modeling system developed by Tim Sheehan, an ecological modeler at CBI. For more information about EEMS and fuzzy logic, or to download the EEMS software package, click here. EEMS is available as a set of script tools in an ArcGIS toolbox, or as a standalone command-line based program. An EEMS manual is included with the software package, but it can also be downloaded separately by clicking here.

A Primer on EEMS & Fuzzy-Logic

Simply put, fuzzy-logic allows you to assign shades of gray to thoughts and ideas rather than being limited to the binary (true/false) determinations of traditional logic. It is this concept of "partial truth" which allows fuzzy-logic models to more accurately capture and resemble human patterns of thought.

EEMS fuzzy-logic models are hierarchical — that is, data flows from the bottom up in order to answer a primary question at the top of the hierarchy. Each node (box) in the hierarchy represents a proposition. A proposition is simply a statement that can either be totally true (+1), totally false (-1), or somewhere in-between at any given location. For example, if the proposition is "High Precipitation", a value of +1 at a specific location would indicate that this statement is totally true at that location (i.e., that there is definitely a high level of precipitation). A value of -1 at a different location would indicate that this statement is totally false (i.e., that there is definitely NOT a high level of precipitation). And values in between -1 and +1 simply represent degrees of truth along a continuum (the gray areas), and can be interpreted as follows:
  • Values greater than Ø indicate that the proposition is more true than false.
  • Values equal to Ø indicate that the proposition is neither true nor false.
  • Values less than Ø indicate that the proposition is more false than true.
The fuzzy (truth) values for each proposition get combined up the tree using various fuzzy-logic operators (e.g., OR, AND, UNION) in order to calculate the fuzzy value for the node directly above. In the example model diagram shown above, we are saying that there is High Precipitation if there is either High Rainfall OR High Snowfall (the OR operator takes the highest value). The numerical values in the boxes represent what the fuzzy values might be at a hypothetical location. In this example, since there is High Rainfall, there is High Precipitation.

Getting Started

To get started with EEMS Online, select a model from the dropdown menu (labeled #1 in the control panel shown below). A short description provides some basic background information about the model. Click on the "Learn more" link for additional information.
Fig.1 - Use the dropdown menu to select a model.
Once you have selected a model, you can use the interactive diagram on the left-hand side of the screen to explore the model, and optionally, make changes to the model. Clicking any node in the diagram will display the corresponding dataset in the map and expand the node to show any input variables. Clicking the gear icon on any node brings up a dialog box that allows you to make changes to the operator, or change the operator to a different operator (Fig 2). The histogram to the right of the operator selection menu shows the distribution of data for the current node. The Y-Axis indicates the number of reporting units that have the corresonding value on the X-Axis. The available options will vary depending on the node's current operator.
Fig.2 - Clicking the gear icon on any node allows you to make changes to the operator.

Available Operators

The table below lists the set available operators, along with the type of data expected as input and a brief description:

OperatorInput DataDescription
ANDFuzzyFinds the AND value of the inputs (minimum value).
   (previously OrNEG in EEMS version 1.0)
CONVERT TO FUZZYRawConverts a field's values into fuzzy values.
Convert To Fuzzy CategoryRawConverts a field's values into fuzzy values by using the user defined category values and matching fuzzy values. Input values that are not in the user defined categories are assigned the user-defined default fuzzy value.
EEMS Convert To Fuzzy CurveRawConverts a field's values into fuzzy values for EEMS (Environmental Evaluation Modeling System), using linear interpolation between user defined points on an approximation of a curve.
DifferenceRawComputes the difference sum for each row of the inputs.
EEMS EMDS AndFuzzyFuzzy logic operator for EEMS (Environmental Evaluation Modeling System). Finds the EMDS AND value of the inputs. The formula is min + [(mean - min) * (min + 1) / 2]
MaxRawFinds the maximum for each row of the input fields.
MeanRawFinds the mean for each row of the input fields.
MinRawFinds the minimum for each row of the input fields.
NotFuzzyLogical NOT for fuzzy modeling. Reverses the sign of values of the input field.
ORFuzzyFinds the truest value of the inputs (maximum value).
SELECTED UNIONFuzzyFinds the union value (mean) of the specified number of TRUEest or FALSEest inputs.
SUMRawComputes the sum of the inputs.
UNIONFuzzyFinds the union value of the inputs (mean value).
Weighted EMDS AndFuzzyFinds the weighted EMDS AND value of the inputs. The formula is min + [(mean - min) * (min + 1) / 2] where the mean is weighted.
WEIGHTED MEANRawFinds the weighted mean for each row of the input fields.
WEIGHTED SUMRawFinds the weighted sum for each row of the input fields. Multiplies each field by its weight before adding. Like a weighted mean without the division.
WEIGHTED UNIONFuzzyFinds the weighted union (mean) for each row of the input fields.
XORFuzzyFinds the fuzzy EXCLUSIVE OR value of the inputs by comparing the two truest values. If both are fully true or fully false, false is returned. Otherwise it applies the formula: (truest value - second truest value) / (full true - full false)

Selecting an Operator

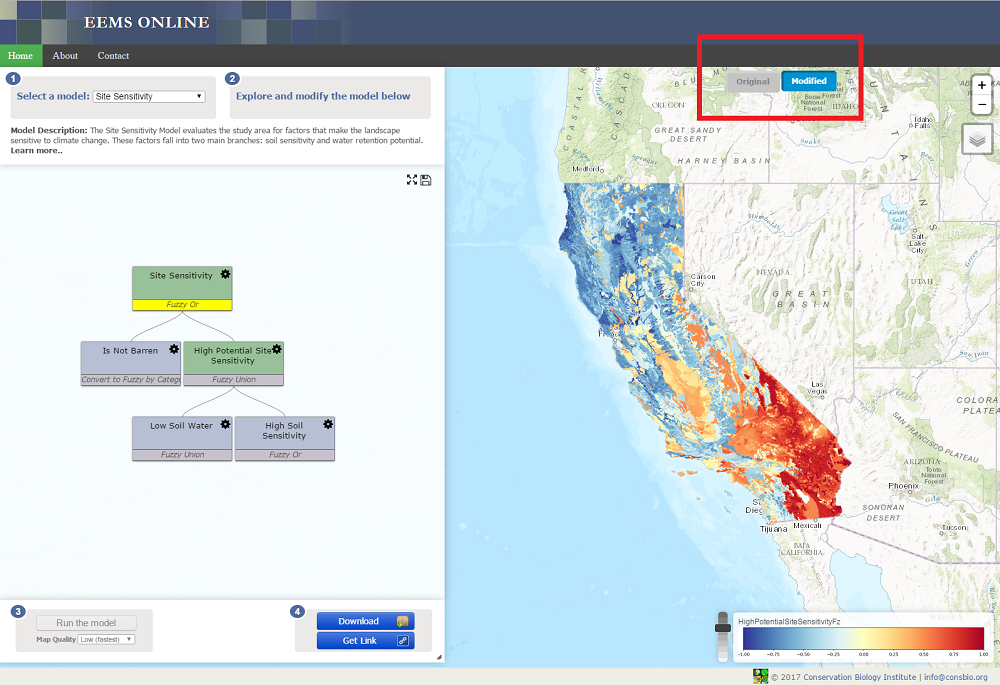
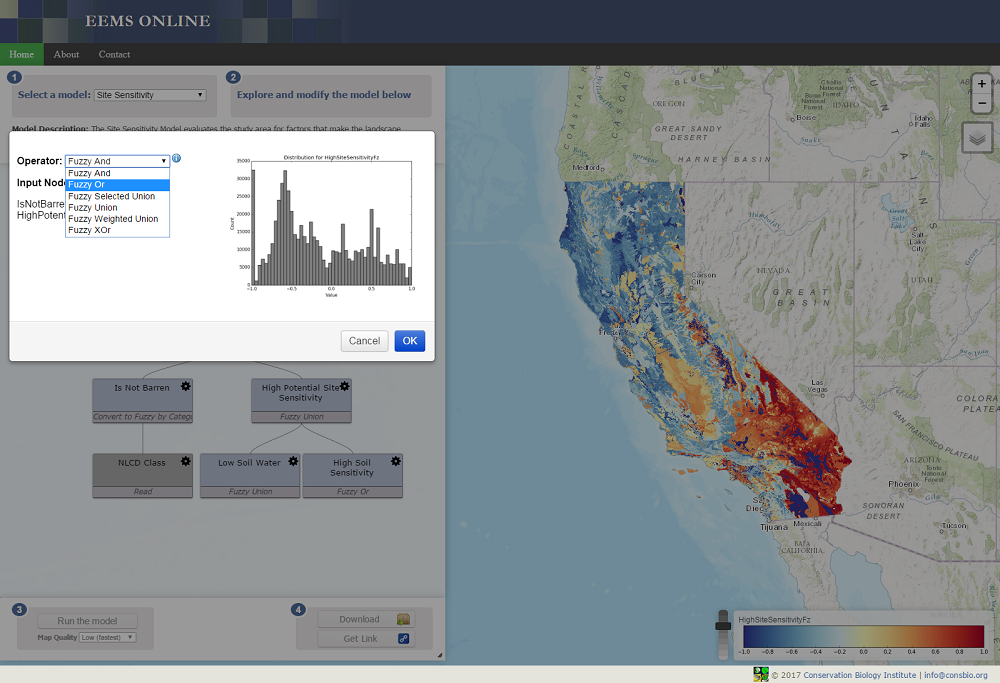
EEMS presents the user with choices for many operators and finding the right one can be confusing at first. The guidelines presented here will help you choose the right operator, but remember, sometimes it is best to experiment with several choices to make sure the operator you choose is appropriate for your model.

EEMS has operators designed to work on data before they are converted into fuzzy numerical space (i.e. when they are still in raw space) and those designed to work on data after they are converted into fuzzy space (see the above table). A user should respect that distinction. Using a non-fuzzy operator on fuzzy data can produce a result that falls outside the -1 to +1 continuum of fuzzy space. Doing this produces an invalid model.

Weighted Sum

The operators used in raw space are for the most part pretty straightforward. However the Weighted Sum operator merits a discussion. A Weighted Sum takes two or more inputs, and multiplies each of them by a weight before adding them. It has proven especially valuable with combining data of very similar types into one result that is then converted into fuzzy space. For example, if you were evaluating a region for intactness, the negative impact of paved roads might be considered similar to but greater than that of dirt roads. Their effects are additive, but a sum operator is not available in fuzzy space. To apply the Weighted Sum operator you might provide a weight of 1 to the paved road density and a weight of 0.5 to the dirt road density. In models that have done this, the result has been labeled “Effective Road Density.”

And, Or, and Union

And, Or and Union are the most common EEMS operators used. The choice between And, Or, and Union depends on the relationship of the input data to the question you are asking. Or returns the highest fuzzy value of any of the inputs, it is appropriate when any of the inputs is sufficient for your desired outcome. For example if you were evaluating a region in which three critically endangered species were present in some locations, you could use an Or to combine presence of species A, presence of species B, and presence of species C into high preserve value. The presence of any of the three species would cause a map reporting unit to have a high fuzzy value. And is used when all inputs are necessary for the result to be high. For instance, if both habitat for and presence of a species of interest were required to consider a location as a preserve, you could combine species presence and habitat density with an And to produce high preservation value. And chooses the lowest fuzzy value of the inputs so that high fuzzy values for both conditions are necessary to yield a high fuzzy value for the result. Union takes the mean of the input values. Union allows each input to exert an influence on the result. If all inputs have a high value, the result will have a high fuzzy value; if all have a low value, the result will be low. If some are high and some are low, the result will be somewhere in between. Going back to our preserve example, we know if the species is present, the location has value as a preserve. If the habitat is present there is some value, too. If they are both present then the value is the highest. Union will yield that result. A Weighted Union is similar to Union, except that it allows a weight to the inputs. In our preserve example, if habitat density is more important than species presence (for instance in an area where remnant populations are under stress and habitat has been restored in areas where the species has not been able to recolonize) then you could provide a greater weight to habitat density.

Selected Union

The Selected Union represents a combination of Or (or And) and Union. Consider a study area that includes many different types of habitat, for example, a basin and range terrain. Some species of concern are found in valleys, others inhabit the foothills, and others the high mountains. What if there are 30 species of concern? The more species of concern in a location, the more valuable the location, but nowhere are they all found together. The Selected Union allows for the evaluation of such a study area. With the Selected Union, you choose a number of the truest (or falsest) of inputs to evaluate. In the basin and range example, you might choose five. A location with a high density of five (or more) species of concern would have a high fuzzy value for high species diversity. As the density of species of concern falls, so does the fuzzy value for high species diversity. A Selected Union with a parameter of 5 Truest would do just that. It performs a Union operation on the five inputs with the highest fuzzy values.

Running the model

You may specify any number of changes to the model. Operators that have been modified will be highlighted in yellow. Once you are satisfied with your changes, click the "Run the model" button labeled #3 on the EEMS Online Control Panel. The model run may take anywhere from several seconds to several minutes to complete, depending on the complexity of the model and the spatial extent and resolution of the input data.

Once the model run is complete, the changes will be reflected in the map. The buttons above the map allow you to change the map display between the original version and the modified version (shown below).
Fig.3 - Use the buttons highlighted above to switch between the original and modified versions of a model run.
Once you have conducted a model run, you have the option of either making additional changes to the model and rerunning it, or, if you are satisfied with the results, you can click the Download button to download the output and associated model content, or push the Get Link button which will allow you to share the modified model or access the modified model through EEMS Online at a later time.